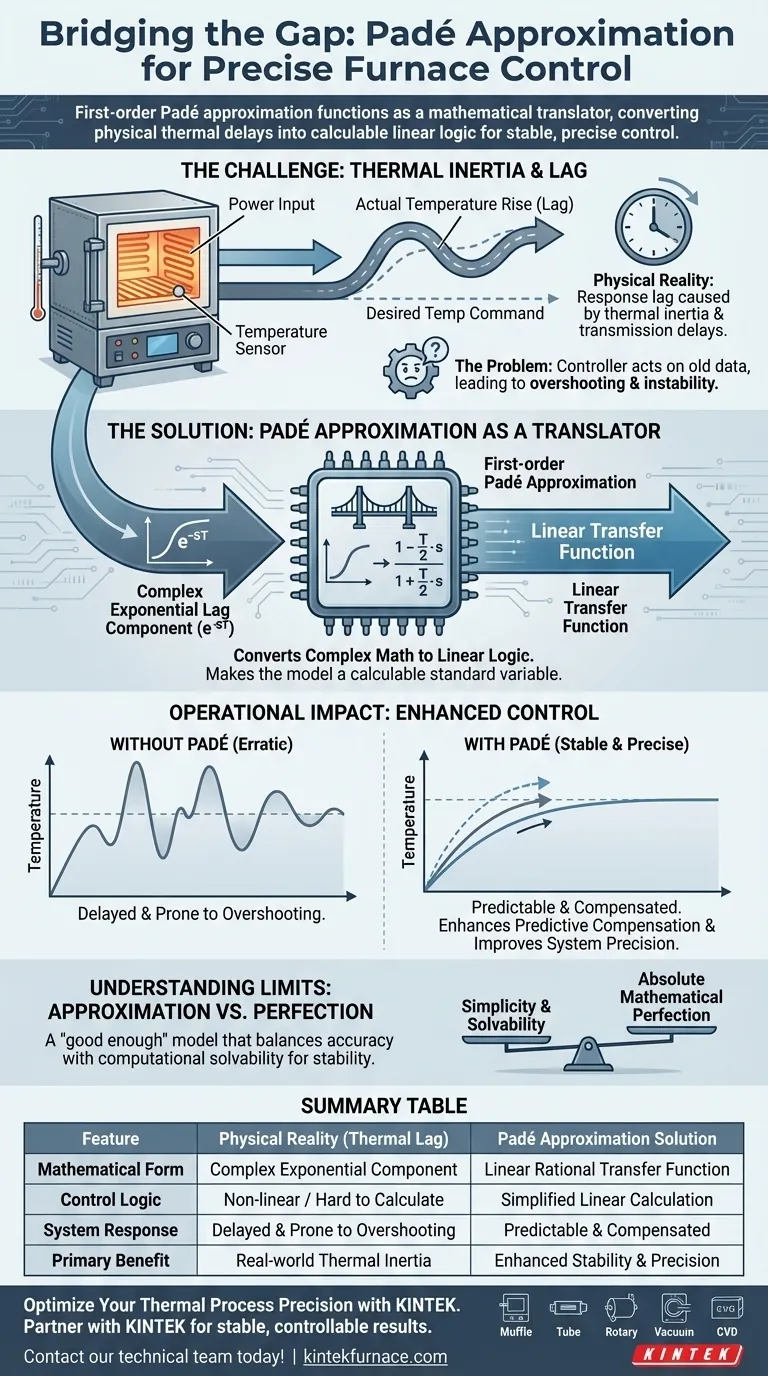
Die Padé-Approximation erster Ordnung fungiert als mathematischer Übersetzer, der die Lücke zwischen physikalischen thermischen Verzögerungen und der Logik des Steuerungssystems schließt. Sie bewältigt technische Herausforderungen bei der Regelung von Elektroöfen, indem sie komplexe exponentielle Verzögerungskomponenten – verursacht durch thermische Trägheit und Übertragungsverzögerungen – in eine berechenbare lineare Übertragungsfunktion umwandelt. Diese Transformation ermöglicht es dem Regler, Verzögerungen effektiv zu kompensieren und sicherzustellen, dass das System stabil und präzise bleibt.
Industrielle Elektroöfen weisen eine erhebliche thermische Trägheit auf, die Zeitverzögerungen verursacht, welche für Standardalgorithmen schwer zu handhaben sind. Die Padé-Approximation erster Ordnung vereinfacht diese komplexen Verzögerungen in ein lineares Format, wodurch das Steuerungssystem das Verhalten zuverlässig vorhersagen und eine präzise Temperaturregelung aufrechterhalten kann.
Die Herausforderung: Thermische Trägheit und Verzögerung
Die physikalische Realität von Elektroöfen
In industriellen Umgebungen reagieren Elektroöfen nicht sofort auf Leistungsänderungen. Es gibt immer eine Reaktionsverzögerung, die durch thermische Trägheit und Übertragungsverzögerungen verursacht wird.
Das Problem mit Zeitverzögerungen
Wenn ein Regler ein Signal zur Erhöhung der Heizleistung sendet, erfolgt der eigentliche Temperaturanstieg später. Diese Übertragungsverzögerung schafft eine Diskrepanz zwischen dem Befehl und dem Ergebnis.
Ohne ordnungsgemäße Modellierung reagiert ein Regler auf alte Daten. Dies führt oft zu einem Überschwingen der Zieltemperatur oder zu Instabilität des Systems.
Wie die Padé-Approximation das Problem löst
Umwandlung komplexer Mathematik in lineare Logik
Mathematisch werden reine Zeitverzögerungen als komplexe exponentielle Verzögerungskomponenten dargestellt. Diese sind in Standardberechnungen von linearen Regelkreisen schwer direkt zu verwenden.
Die Padé-Approximation erster Ordnung löst dieses Problem, indem sie den Exponentialterm in eine lineare Übertragungsfunktion umwandelt. Sie erstellt einen mathematischen rationalen Bruch, der die Verzögerung annähert.
Berechenbarkeit des Modells
Nach der Umwandlung wird die Verzögerung zu einem handhabbaren Teil der Systemgleichung. Der Steuerungsalgorithmus kann die Verzögerung nun als Standardvariable und nicht als komplexe Anomalie verarbeiten.
Auswirkungen auf die Temperaturregelung im Betrieb
Verbesserung der vorausschauenden Kompensation
Durch die Linearisierung der Verzögerung kann der Ofenregler zuverlässiger vorhersagen, wie die Temperatur im Laufe der Zeit reagieren wird. Er kann die Verzögerung "kommen sehen" und die Leistung frühzeitig anpassen, um sie zu kompensieren.
Verbesserung der Präzision und Stabilität des Systems
Das Endergebnis ist ein robusteres System. Da der Regler die thermische Trägheit genau berücksichtigt, werden unregelmäßige Schwankungen vermieden.
Dies führt zu verbesserter Präzision und Stabilität im tatsächlichen Betrieb und stellt sicher, dass der Ofen die richtige Temperatur ohne ständige Oszillationen hält.
Verständnis der Grenzen der Approximation
Approximation vs. Perfektion
Es ist wichtig zu bedenken, dass diese Methode eine Approximation und keine exakte Nachbildung der physikalischen Verzögerung ist. Sie vereinfacht die unendliche Reihe einer Exponentialfunktion zu einem endlichen linearen Verhältnis.
Abwägung zwischen Einfachheit und Genauigkeit
Obwohl sie zur Stabilisierung von Standard-Ofenregelkreisen sehr effektiv ist, tauscht sie absolute mathematische Perfektion gegen rechnerische Lösbarkeit. Sie liefert ein Modell, das "gut genug" ist, um Stabilität zu gewährleisten, ohne übermäßige Rechenleistung zu erfordern.
Die richtige Wahl für Ihre Regelungsstrategie
Bei der Entwicklung oder Abstimmung eines Temperaturregelungsmodells für einen Elektroofen sollten Sie berücksichtigen, wie diese Approximation mit Ihren spezifischen Zielen übereinstimmt.
- Wenn Ihr Hauptaugenmerk auf Systemstabilität liegt: Verwenden Sie die Padé-Approximation, um Schwingungen zu vermeiden, die durch die Verzögerung zwischen Heizelement und Sensor verursacht werden.
- Wenn Ihr Hauptaugenmerk auf Algorithmus-Einfachheit liegt: Implementieren Sie diese Methode, um komplexe nichtlineare Verzögerungsmatrizen in eine standardmäßige lineare Funktion umzuwandeln, die einfach zu berechnen ist.
Indem Sie physikalische Verzögerungen in einen linearen mathematischen Wert umwandeln, verwandeln Sie eine chaotische thermische Reaktion in einen vorhersagbaren, steuerbaren Prozess.
Zusammenfassungstabelle:
| Merkmal | Physikalische Realität (Thermische Verzögerung) | Padé-Approximation Lösung |
|---|---|---|
| Mathematische Form | Komplexe Exponentialkomponente | Lineare rationale Übertragungsfunktion |
| Regelungslogik | Nichtlinear / Schwer zu berechnen | Vereinfachte lineare Berechnung |
| Systemreaktion | Verzögert & anfällig für Überschwingen | Vorhersagbar & kompensiert |
| Hauptvorteil | Reale thermische Trägheit | Verbesserte Stabilität & Präzision |
Optimieren Sie die Präzision Ihres thermischen Prozesses mit KINTEK
Die Überwindung thermischer Trägheit erfordert sowohl mathematische Präzision als auch Hochleistungs-Hardware. KINTEK bietet branchenführende Heizlösungen, die durch erstklassige F&E und Fertigung unterstützt werden. Ob Sie Muffel-, Rohr-, Dreh-, Vakuum- oder CVD-Systeme benötigen, unsere Labor-Hochtemperaturöfen sind vollständig anpassbar, um Ihre individuellen Anforderungen an die Temperaturregelung zu erfüllen.
Lassen Sie nicht zu, dass Reaktionsverzögerungen Ihre Ergebnisse beeinträchtigen. Arbeiten Sie mit KINTEK zusammen, um die Stabilität und Kontrolle zu erreichen, die Ihre Forschung erfordert. Kontaktieren Sie noch heute unser technisches Team, um Ihre individuellen Ofenanforderungen zu besprechen!
Visuelle Anleitung
Referenzen
- Serdar Ekinci, Євген Зайцев. Efficient control strategy for electric furnace temperature regulation using quadratic interpolation optimization. DOI: 10.1038/s41598-024-84085-w
Dieser Artikel basiert auch auf technischen Informationen von Kintek Furnace Wissensdatenbank .
Ähnliche Produkte
- 1200℃ Kontrollierter Ofen mit Stickstoffatmosphäre
- 1700℃ Gesteuerter Ofen mit inerter Stickstoffatmosphäre
- 1400℃ Gesteuerter Ofen mit inerter Stickstoffatmosphäre
- 1200℃ geteilter Rohrofen Labor-Quarzrohrofen mit Quarzrohr
- Spark-Plasma-Sintern SPS-Ofen
Andere fragen auch
- Wie funktioniert ein chargenbeheizter Ofen mit kontrollierter Atmosphäre? Meistern Sie Präzisionswärmebehandlung für überlegene Materialien
- Was sind die Anwendungsgebiete von Inertgasöfen? Unverzichtbar für Metallverarbeitung, Elektronik und Additive Fertigung
- Welche Vorteile bietet die Wärmebehandlung unter inerter Atmosphäre? Oxidation verhindern und Materialintegrität bewahren
- Was ist der Hauptzweck der Wärmebehandlung? Metallische Eigenschaften für überlegene Leistung umwandeln
- Was sind die Hauptvorteile eines experimentellen Kammerofens mit kontrollierter Atmosphäre? Erzielen Sie eine präzise Umweltkontrolle für fortschrittliche Materialien
